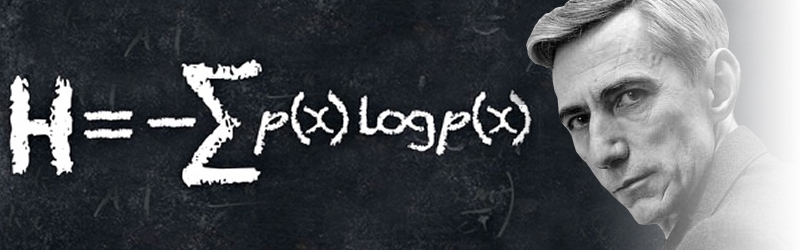عدد بعدی چیست؟
در بخش های اول و دوم و سوم تا جایی پیش رفتیم که هرمان هولریث از دستگاه دودویی برای اختراع خود استفاده کرد که با این کار نگاه بشر به این ایده باز شد.
همانطور که گفتیم سال 1854، «جورج بول» (George Boole) مفهومی منطقی موسوم به «جبر بولی» را پیشنهاد کرد؛ زیرمجموعه ای از علم جبر که در آن ورودی و خروجی عملیات منطقی تنها می توانستند دو مقدار داشته باشند: درست و غلط . البته این امکان هم وجود داشت که مقادیر صفر و یک به آنها اختصاص داد. این واقعیت که مدارهای رله ی دودویی (سوییچ های ساده ای که با جریان الکتریکی کنترل می شدند) را می توان در نقش «دروازه های کنترلی» برای انجام عملیات های بولی استفاده کرد، عموما به ریاضیدان و مهندس آمریکایی «کلود شانون» (Claude Shannon) نسبت داده می شود که پایان نامه ی دانشگاهی اش در سال 1937 ، تاثیر و نفوذ مهمی در این زمینه بر جای گذاشت.
اصول نظری کار خیلی ساده بود. چیدمان صحیح رله ها می تواند خروجی ای تولید کند که با دو مقدار ورودی کنترل می شود. برای نمونه، یک دروازه ی «و» (AND) تنها در صورتی سیگنال را عبور می داد که جریانی الکتریکی در هر دو ورودی اش وجود داشت، اما برای تولید سیگنال خروجی در یک دروازه ی «یا» (OR) کافی بود تنها در یکی از ورودی ها جریان وجود داشته باشد. شبکه های متشکل از تعداد زیادی از این دروازه های منطقی قادر به انجام محاسبات بودند و عملیات های منطقی پیچیده را با سرعتی بالا روی مجموعه ای از ارقام دودویی انجام می دادند.
با وجود این همزمان افراد دیگری هم با ایده ی استفاده از رله ها برای ساخت کامپیوتر از راه رسیدند. در همان سال 1937 ، محققی به نام «جورج استیبیتز» (George Stibitz) که در مجموعه ی «آزمایشگاه های بل» در نیوجرسی آمریکا کار می کرد، شبکه ی منطقی ساده ای را با استفاده از مجموعه ای از رله و لامپ رشته ای روی میز آشپزخانه اش سرهم کرد. سال بعد، روسای استیبیتز در آزمایشگاه بل از او خواستند دستگاهش را به شکل یک دستگاه محاسباتی الکترومکانیکی کامل توسعه دهد. به این ترتیب، کامپیوتر «Complex Number» در ژانویه ی 1940 تکمیل شد که تا سال 1949 هم مشغول کار بود، اما از آن جا که قابل برنامه ریزی نبود، نمی توان آن را یک کامپیوتر واقعی دانست.
در همین زمان و در سوی دیگر اقیانوس اطلس، «کنراد زوس» (Conrad Zuse)، مهندس و علاقه مند علوم محاسباتی، مشغول کار روی مسئله ی مشابهی بود.
در سال 1938، زوس با بودجه ای محدود، یک ماشین محاسب دودویی به نام«Z1» ساخت که کاملا مکانیکی بود. طی چند سال بعد و با سرمایه گذاری ارتش آلمان، زوس ماشین «Z2» و در سال 1941 ماشین «Z3» را ساخت. دستگاه سوم به جای سوییچ های مکانیکی از رله های الکترومکانیکی استفاده می کرد و به مراتب قابل اعتمادتر بود. اما با اوج گیری جنگ جهانی دوم، اولویت های ارتش آلمان تغییر کرد و به همین دلیل با درخواست بودجه ی زوس برای جایگزینی رله های دستگاهش با لامپ های تمام الکترونیکی مخالفت کردند.
ادامه دارد...
منابع:
کتاب 6 نظریه ای که جهان را تغییر داد، اثر پل استراترن
کتاب آشنایی با آلن تورینگ، اثر پل استراترن
مجله دانستنیها شماره 182
در بخش پیش تا اختراع مهم ماری ژاکارد پیش رفتیم. روش ژاکارد هنوز هم برای بافتن الگوهای پیچیده به کار می رود. ماشین های حساب مکانیکی پیچیده، مفهوم برنامه نویسی، تئوری اعداد حساب کردنی - یعنی عناصر اصلی کامپیوتر های مدرن - داشتند ظاهر می شدند. اما فقط یک نابغه تشخیص داد که چگونه این عناصر مجزا را می توان با همدیگر ترکیب کرد. « چارلز بابیج » را عموما پدر کامپیوتر می شناسند. مانند هر نابغه ای در زمینه های عملی، او بدجوری به معنی واقعی کلمه غیرعملی بود. اما اکتشافات و دستاورد های او یک قرن جلوتر از زمانش بود.
بابیج در سال 1791 متولد شد و ثروت فراوانی را به ارث برد. او که جوان مهربانی بود به سرعت استعدادی استثنایی در زمینه ی ریاضیات نشان داد. او به طور موفقیت آمیزی برای معرفی حساب لایب نیتز به بریتانیا فعالیت کرد.
بابیج خود را متوجه مشکل دیگری کرد که دانشمندان بریتانیایی را به زحمت انداخته بود - یعنی اشتباه های مکرری که در چاپ جدول های ریاضی و ستاره شناسی به وفور دیده می شد. مثلا چاپ اول جدول های دریایی برای تعیین طول و عرض جغرافیایی در دریا حاوی بیش از هزار اشتباه بود.
بابیج اعتقاد داشت که برای حل مسئله ی جدول های اشتباه فقط یک پاسخ وجود دارد. لازم بود تا یک ماشین محاسبه بزرگ، چند منظوره و بدون خطا ساخته شود. بابیج پس از موفقیت در دریافت کمک از دولت بر آن شد تا «ماشین تفاضل شماره 1» مشهور خود را بسازد. این کار بسیار عظیم و بلندپروازانه ای بود. ماشین بابیج نه تنها قرار بود بتواند تا 20 رقم را محاسبه کند، بلکه قرار بود یک ررشته اعداد را هم حفظ کند و آن ها را جمع بزند. محاسبات ماشین به جمع زدن محدود می شد، زیرا از شیوه ی مجموع تفاضل ها استفاده می کرد. در این روش از چند جمله ای ها (فرمول های جبری که حاوی چندین عبارت هستند) و این واقعیت که دارای یک اختلاف ثابت هستند استفاده می شود. به عبارت ساده تر:
اگر:
f(x) = 2x + 1
x = 1 2 3 4 ...
f(x) = 3 5 7 9 ...
... 2 2 2 2=تفاضل
واضح است که استفاده از این روش در مورد محاسبات پیچیده آن قدر ها آسان نیست. اما در اینجا یک تفاضل ثابت ممکن است در تفاضل بین تفاضل ها پیدا شود ( یا تفاوت بین تفاوت بین تفاوت ها ) . در بیشتر موارد اگر چندجمله ای عبارت xn را داشته باشد، پیش از پیدا کردن اختلاف ثابت باید n بار تفاوت محاسبه شود. برای محاسبه یک چندجمله ای برای یک سری از مقادیر x ، چنانکه برای تشکیل یک جدول لازم است، برای یک ماشین بسیار آسان تر است تا تفاضل ثابت را جمع کند و با افزودن تفاضلی دیگر به عقب بازگردد _ تا این که وارد یک رشته عملیات ضرب کردن پیچیده شود. و عملیات لگاریتمی و مثلثاتی را، که به این ترتیب نیستند، می توان با تقریب نزدیکی به چند جمله ای های ساده تری کاهش داد.
« ماشین تفاضل شماره 1 » ( مانند ماشین حساب های پیش از آن ) از چرخ های دندانه داراستفاده می کرد و بر اساس سیستم دهدهی کار می کرد _ ولی ساختمان آن از لحاظ پیچیدگی بسیار پیشرفته تر از بقیه ی ماشین ها بود و یک رشته ابداعات در زمینه ی مهندسی مکانیک لازم داشت.
اما بابیج که در گذشته استاد تهیه ی چیز ها با امکانات کم بود، آماده این وظیفه بود. هم چنان که ماشین او بزرگتر می شد، او فکر های بهتری برای خصوصیات ابداعی ماشین پیدا می کرد و همچنان که پیش می رفت آن ها را در ماشین اعمال می کرد. «ماشین تفاضل شماره 1» در سال 1823 شروع شد، ولی هیچ تکمیل نشد. پس از 10 سال کار بابیج طرح اولیه خود را به ماشینی با 25000 قطعه افزایش داد (که فقط 12 هزار قطعه ی آن ساخته شده بود) و هزینه ی به 17470 پوند افزایش یافته بود (که در آن روزگار با این پول می شد که یک چند کشتی جنگی ساخت). بابیج مقدار زیادی از این مبلغ را از جیب خودش پرداخته بود، ولی دولت تصمیم گرفت تا این برنامه را متوقف کند. بهتر بود که در نیروی دریایی سرمایه گذاری کرد تا ماشینی که با ارقامی قرض ملی را افزایش می دهد که فقط خودش می تواند آن را محاسبه کند. با همه ی این مشکلات ، در سال 1827 بابیج فقط از بخش قابل استفاده ای از این ماشین (که فقط از 2000 قطعه درست شده بود) استفاده کرده بود که جدول های لگاریتمی از 1 تا 108000 را محاسبه می کرد. این بخش قابل استفاده از «ماشین تفاضل شماره 1» را عموما اولین ماشین حساب محسوب می کنند. اعداد به ماشین داده می شدند و پاسخ ها به شکل چاپ شده بیرون می آمدند (و بدین ترتیب احتمال خطای انسانی را از میان می بردند).
اما تا آنجایی که به بابیج مربوط می شد این تازه آغاز کار بود. در سال های 1830 او طرح «ماشین تفاضل شماره 2» را در سر داشت. این مفهوم پیشرفت قابل ملاحظه ای در تکنیک محاسبه بود. این اولین ماشین آنالیتیک می بود. ماشینی که کارکرد آن توسط یک برنامه ی خارج از آن کنترل می شد. بابیج از کارت های سوراخ دار ژاکارد برای کنترل مکانیسم یک ماشین آگاه بود و تصمیم گرفت از این شیوه در ماشین های خودش استفاده کند. این روش او را قادر می ساخت تا هرگونه کارهای محاسباتی را براساس دستورهایی انجام دهدکه توسط کارت های سوراخدار در ماشین گذاشته می شد. این ماشین همانند «ماشین تفاضل شماره 1» حافظه ای داشت که می توانست با این اعداد ضبط شده یک ردیف عملیات مختلف انجام دهد. بابیج خصوصیات اساسی کامپیوتر های مدرن را ابداع کرده بود.
هسته ی اصلی، که همه ی این خصوصیات به آن متصل می شد، قطعه ی مقاومت بود. این هسته شامل 1000 میله ی محوری و بیش از 50هزار چرخ دنده بود و می توانست با استفاده از دستگاه دهدهی اعداد 50 رقمی را محاسبه کند.
متاسفانه دولت انگلستان از تسلیم دربرابر چنین امکانات عظیمی خودداری کرد و با دومین کوشش جهت ورشکسته کردن خزانه ی دولت مخالفت کرد و ماشین تفضل شماره 2 ساخته نشد.
پس از درگذشت چارلز بابیج در سال 1871، طرح او برای ماشین تفاضل شماره 2 برای چندین سال فراموش شد. بعد ها هسته ی اولین موتور آنالیتیکی بر طبق نقشه ی اصلاح شده «ماشین تفاضل شماره 2» ساخته شده. این دستگاه باشکوه 3 تنی را اکنون با تمام عظمت آن می توان در موزه ی علوم لندن تماشا کرد. و کار هم میکند. ( هنگام آزمایش آن 25 مضرب عدد پی را تا 29 رقم اعشاری به آن دادند تا حساب کند _ کاری که 50000 چرخ دنده آن با کمال آسانی انجام دادند.)
ادامه دارد...
منابع:
کتاب 6 نظریه ای که جهان را تغییر داد، اثر پل استراترن
کتاب آشنایی با آلن تورینگ، اثر پل استراترن
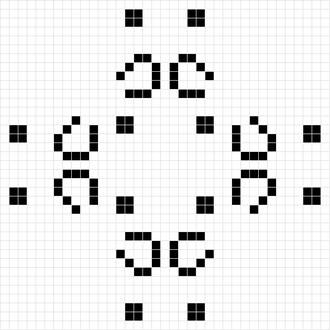
دنیای بازی زندگی از یک جدول نامتناهی دو بعدی با بردارهای متعامد ساخته شدهاست که شامل سلولهای مربع شکل است. هر سلول میتواند یکی از دو حالت زنده و یا مرده را داشته باشد. هر سلول با هشت سلول همسایه و همجوار خود به صورت افقی، عمودی و مورب، در تراکنش است. در هر مرحله زمانی از بازی، تحولات زیر اتفاق میافتند:
- ۱. هر سلول زنده با کمتر از ۲ همسایه زنده، میمیرد. (به دلیل کمبود جمعیت)
- ۲. هر سلول زنده با بیش از ۳ همسایه زنده، میمیرد. (به دلیل ازدحام جمعیت)
- ۳. هر سلول زنده با ۲ و یا ۳ همسایه زنده، زنده میماند و به نسل بعد میرود.
- ۴. هر سلول مرده با دقیقاً ۳ همسایه زنده، دوباره زنده میشود.
الگوی آغازین بازی به عنوان بذر سیستم به حساب میآید. اولین نسل در بازی با اعمال قوانین فوق بر تک تک سلولها به صورت همزمان ایجاد میشود و در آن زاد و ولدها و مرگ و میرها اتفاق میافتد. این رویه تا ایجاد نسلهای آینده ادامه مییابد. بدین ترتیب هر نسل تابعی از نسل ما قبل خود خواهد بود.
اگر این بازی را مثلا تا 10هزار مرحله انجام دهیم به نتایج بسیار شگفت آور و جالبی دست می یابیم. برای مثال، حتی اگر مهره ها را در ابتدای بازی کاملا نامنظم چیده باشیم، ساختار های بسیار پیچیده و منظمی شکل می گیرند، برای مدتی باقی می مانند، هر از گاهی تولید مثل می کنند و سرانجام از بین می روند. علاوه بر اینها، دو پدیده چشم گیر نیز مشاهده می شود: یکی اینکه هرقدر بازی را ادامه می یابد، ساختارهای ساده به سازه های پیچیده تبدیل می شوند (تکامل می یابند). مثلا ، همانگونه که در زیر می بینیم، از بی نظمی خود به خود به خاطر چند قانون ساده ، نظم به وجود می آید.
نه تنها پدیده دوم بسیار مهم تر است، بلکه موجوداتی که شکل می گیرند (یا متولد می شوند) رفتار ها و خصلت های خاصی از خود نشان می دهند که مشابه رفتار و خصوصیاتی است که در موجودات زنده مشاهده می شوند و جالبتر اینکه پاره ای از آنها را خصایص ذاتی یا غریزی می دانیم. در این بازی ساختارها (یا موجوداتی) شکل می گیرند که با وجود بزرگ یا کوچک شدنشان، یکپارچگی خود را حفظ می کنند. بعضی از این ساختارها هرچه در زمان جلوتر می روند مهره هایی را پشت سر خود به جا می گذارند. برخی دیگر، تا بزرگ می شوند، موجودات کوچک تری در اطرافشان ظاهر می شوند که شروع به خوردن آنچه از موجود بزرگتر بر جای مانده میکنند ( از موجود بزرگتر تغذیه می کنند ) و جالبتر اینکه اگر از خوردن آنها جلوگیری شود، راه موجود بزرگتر را سد میکنند. ( مشابه بچه ای که اگر مادرش به او غذا ندهد مزاحمش می شود) و در نهایت اگر باز هم غذا به آنها نرسد موجود بزرگتر را تکه تکه می کنند.
نکته مهم و شاید باور نکردنی این است که 3 قانون این نظم را از این بی نظمی در می آورد و شاید جهان ما نیز تنها با چند قانون ساده به پیچیدگی حال رسیده باشد.
منابع:
کتاب صفر اثر دکتر مسعود ناصری
ویکیپدیا
www.conwaylife.com